Layer Normalization

Essential AI Math Excel Blueprints

\(\begin{align} \mu^{(i)} = \frac{1}{D} \sum_{j=1}^{D} x_{j}^{(i)} \\ \sigma^{2^{(i)}} = \frac{1}{D} \sum_{j=1}^{D} \left(x_{j}^{(i)} - \mu^{(i)}\right)^2 \\ \hat{x}_{j}^{(i)} = \frac{x_{j}^{(i)} - \mu^{(i)}}{\sqrt{\sigma^{2^{(i)}} + \epsilon}} \\ y_{j}^{(i)} = \gamma_j \hat{x}_{j}^{(i)} + \beta_j \\ \end{align}\)

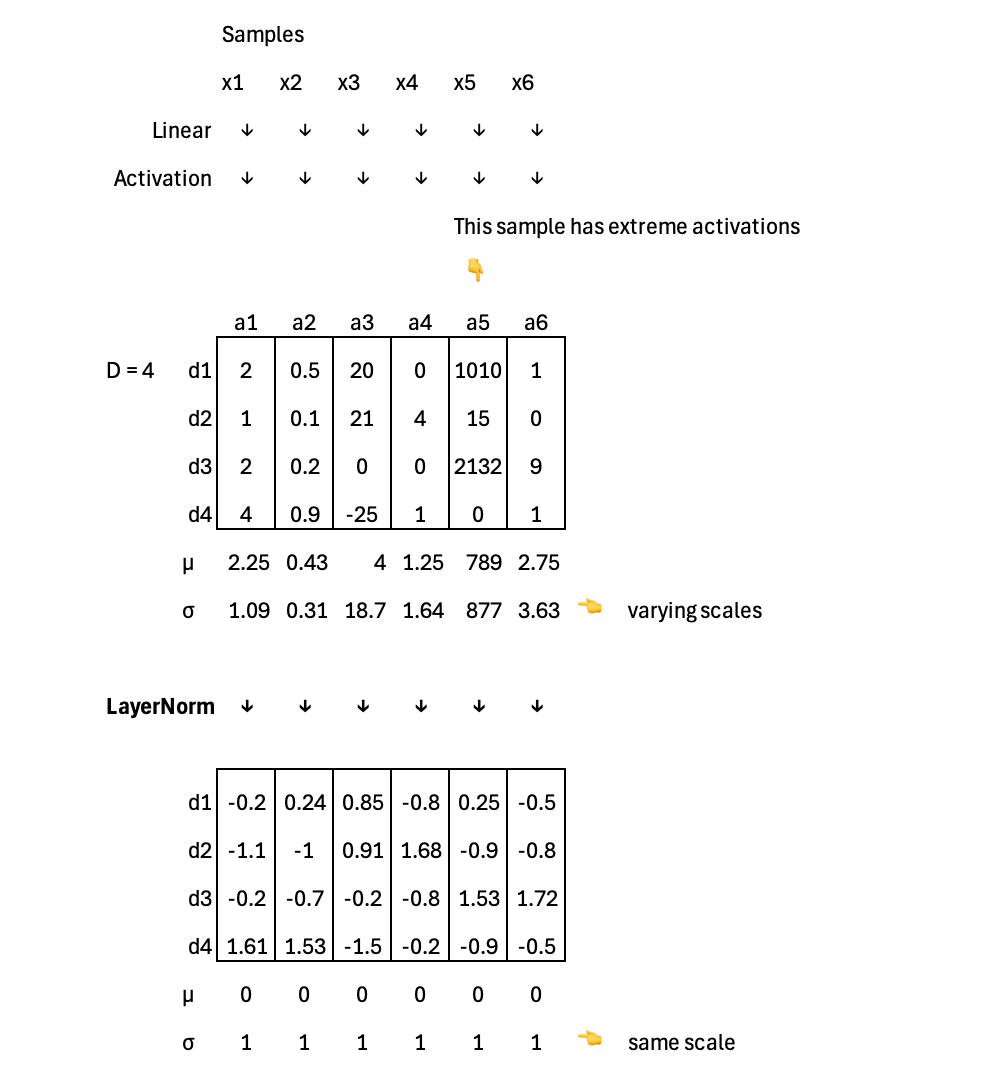
Layer normalization is used to stabilize training when individual samples exhibit extreme activations and highly varying scales within a layer. For a given input, some features may spike to very large values while others remain small, causing a single sample’s activation vector to be poorly scaled and dominated by a few components. Layer normalization computes statistics across features within each sample, rescaling activations to a consistent scale so no single feature overwhelms the computation in that forward pass. This makes optimization more stable and is especially effective when mini-batch sizes are small or batch statistics are unreliable.

Excel Blueprint

This Excel Blueprint is available to AI by Hand Academy members. You can become a member via a paid Substack subscription.