Sinusoidal Positional Encoding
Essential AI Math
Sinusoidal positional encoding gives a model a sense of token order in architectures that process all tokens in parallel. By adding sine and cosine signals of different frequencies to each token embedding, it encodes both absolute position and relative distance between tokens. This allows the model to reason about sequence order (e.g., “next” or “farther away”) and generalize to longer sequences without learning position-specific parameters.
Calculation
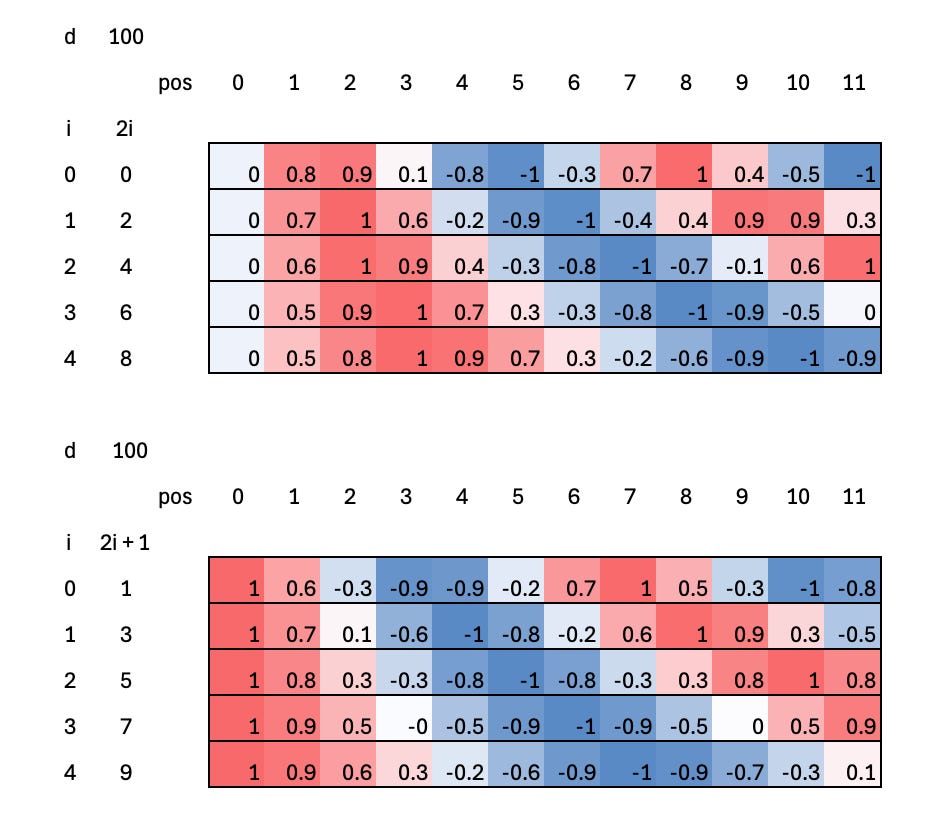
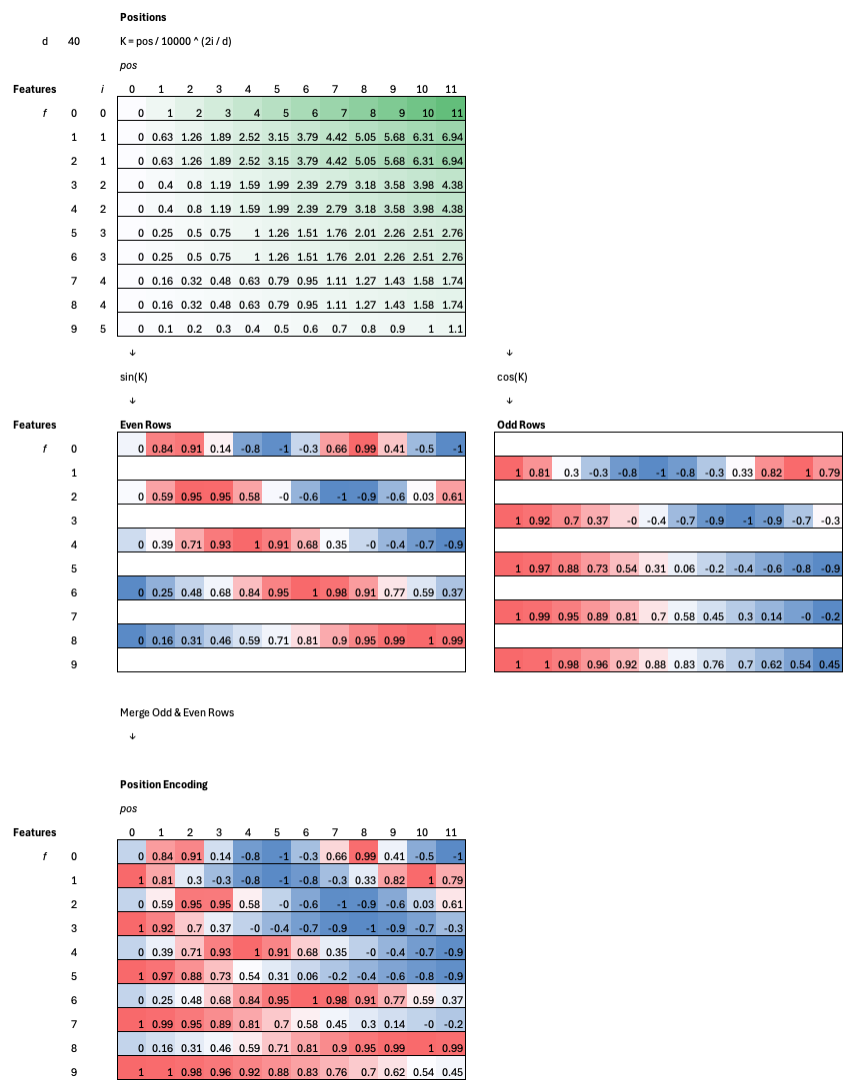
For each token position, we compute a positional encoding vector using sine and cosine functions at different frequencies. Even-indexed rows (dimensions) use a sine function, while odd-indexed rows use a cosine function, both scaled by a power of 10,000 so that each dimension varies at a different rate.
Application
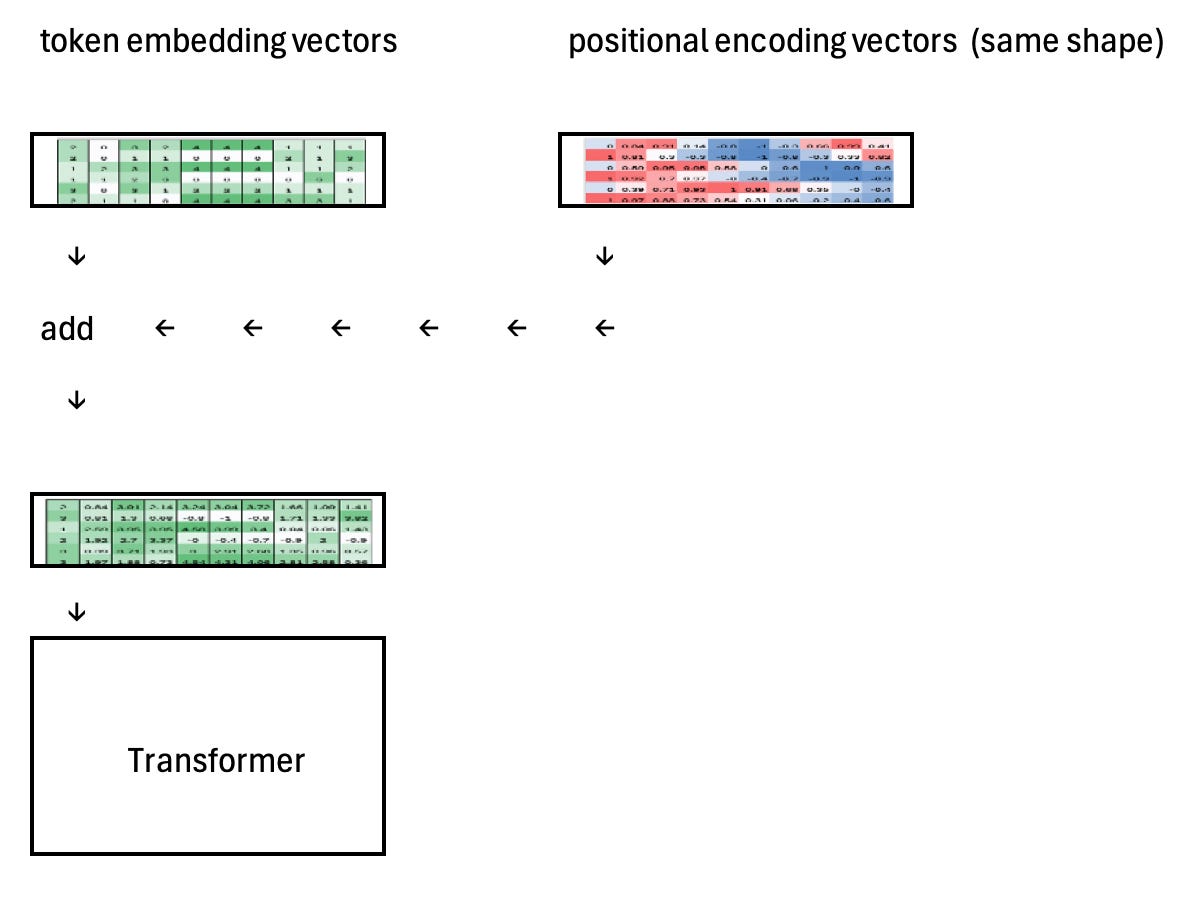
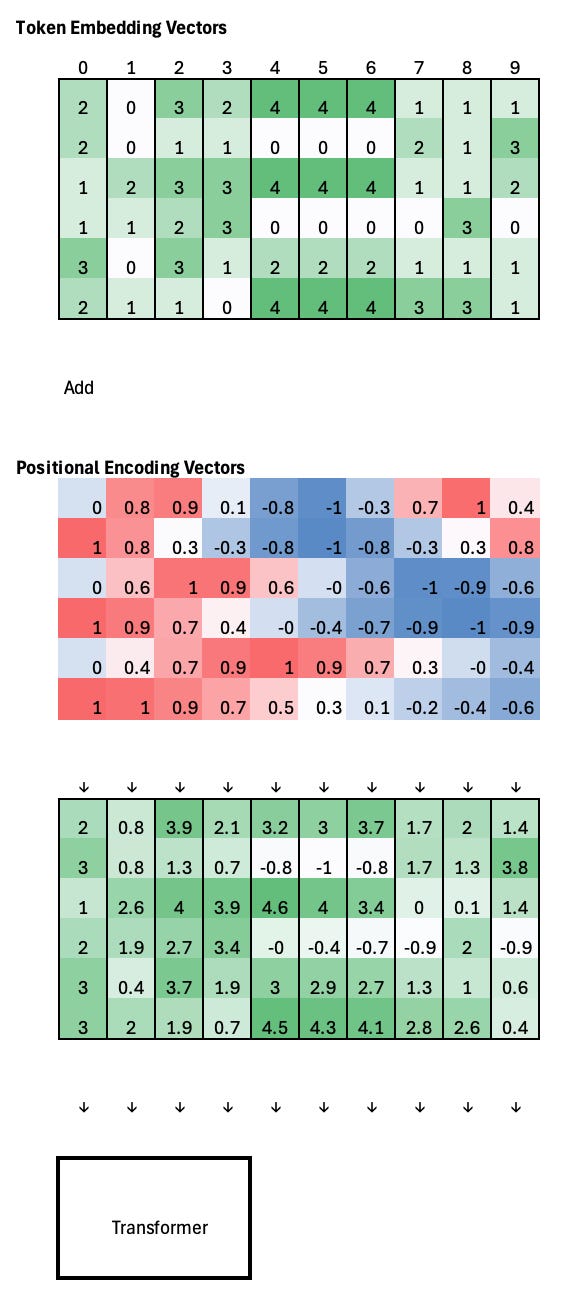
The most common use of sinusoidal positional encoding in a Transformer is to add it directly to the token embeddings before they are fed into the attention layers. Token embeddings capture what each token is, while the sinusoidal signals encode where each token appears in the sequence. By summing the two vectors element-wise, the model receives both content and position information in a single representation, allowing attention to reason about order and relative distance without changing the Transformer’s architecture or adding learned positional parameters.
For example, if the token embedding vectors at positions 4, 5, and 6 are identical, the Transformer has no way to distinguish their order on its own. After adding sinusoidal positional encodings, each embedding is shifted by a slightly different positional vector, making the representations distinct. Importantly, these shifts are smooth and structured, so the overall geometry of the embedding space is preserved while position information is injected.
Excel Emulation of PyTorch Code
1 import torch
2 seq_len = 10
3 d_model = 16
4
5 pe = torch.zeros(d_model, seq_len)
6 position = torch.arange(seq_len)
7 dim_index = torch.arange(0, d_model, 2)
8 scale = -math.log(10000.0) / d_model
9 div_term = torch.exp(dim_index * scale)
10 angles = div_term[:, None] * position[None, :]
11
12 # even dimensions ↓ (sine)
13 even = torch.sin(angles)
14 # odd dimensions ↑ (cosine)
15 odd = torch.cos(angles)
16
17 pe[0::2, :] = even
18 pe[1::2, :] = oddTo inspect and interact with the formulas 👉 🔗 View the Excel Blueprint Online
Previous issues in the series:



Excellent breakdown of positional encoding mechanics. The frequency scaling insight is crucial because lower dimensions capture coarse patterns while higher ones encode fine-grained position details. Back when I was implementing custom transformers, the smooth geometric preservation part tripped me up until Iunderstood why the sinusoids dont disrupt embedding space topology.